Other
Scheimpflug optics
Scheimpflug optics are a special class of lenses, either of the fixed focal, macro or telecentric type, designed to meet the Scheimpflug criterion.
Suppose that the object plane of an optical setup is not parallel to the image plane (e.g. a camera-lens system imaging a flat target at 45°): this causes the image to be sharp only where the focus plane and the target plane intersect. Since the image and object planes are conjugated, tilting the first plane by a certain angle will also cause the latter to tilt by a corresponding angle. Once the focus plane is aligned to the target plane, focus across the image is restored.
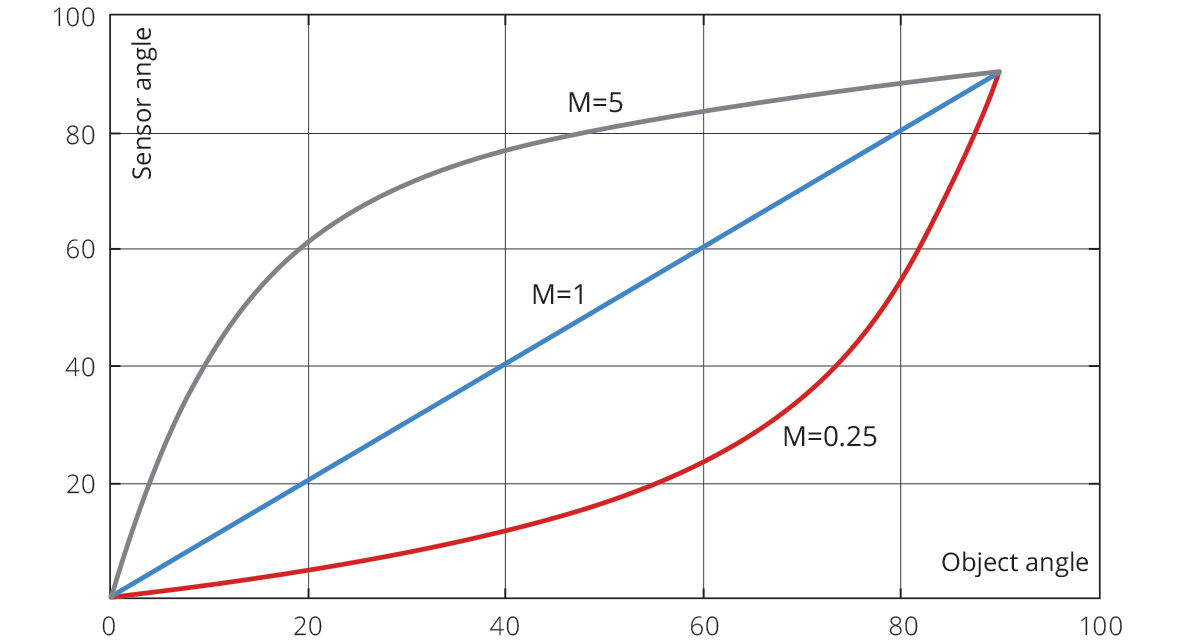
The angle at which the sensor plane must be tilted is given by the Scheimpflug criterion:
where M is the lens magnification, θ’ is the image plane tilt angle (i.e. on the sensor side) and θ is the object plane tilt angle.
It is clear that at high magnifications this condition is impossible to meet, since an object plane tilted by 45° would require to tilt the sensor by 80°, causing severe mechanical and vignetting issues (see picture, where M=5 black, M=1 blue, M=0.25 red).
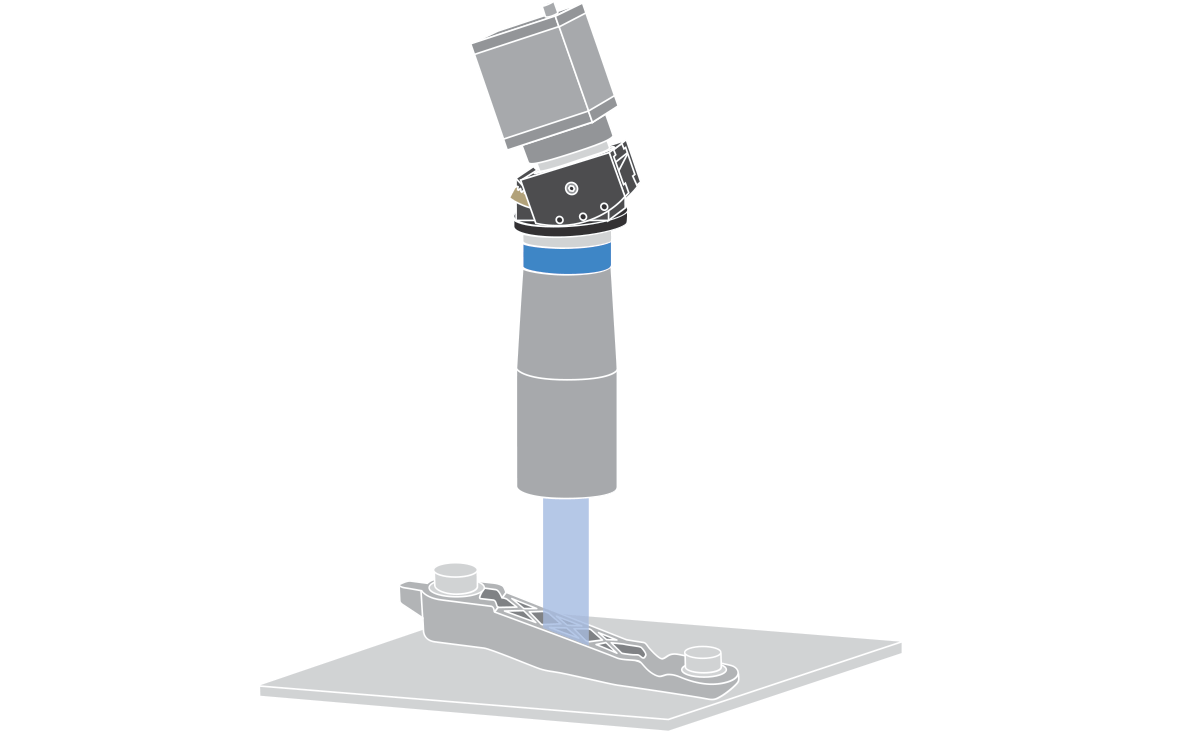
Image plane tilting is practically realized by changing the angle of the camera with respect to the optics by means of special tiltable mounts: the picture below illustrates an example of a Scheimpflug telecentric setup.
IR Optics
In machine vision, we find a number of interesting and high tech applications of IR radiation: the imaging process in some regions of the spectrum requires specifically designed lenses called IR optics.
All objects with an absolute temperature over 0 K emit infrared (IR) radiation. Infrared radiant energy is determined by the temperature and emissivity of an object and is characterized by wavelengths ranging from 0.76 μm (the red edge of the visible range) to 1000 μm (beginning of microwaves range). The higher the temperature of an object, the higher the spectral radiant energy, or emittance, at all wavelengths and the shorter the peak wavelength of the emissions. Due to limitations on detector range, IR radiation is often divided into three smaller regions based on the response of various detectors.
SWIR (0.9-1.7 μm) is also called the «reflected infrared» region since radiation coming from a light source is reflected by the object in a similar manner as in the visible range.
SWIR imaging requires some sort of illumination in order to image an object and can be performed only if some light, such as ambient moonlight or stars light is present. In fact, the SWIR region is suitable for outdoor, night-time imaging. SWIR imaging lenses are specifically designed, optimized, and anti-reflection coated for SWIR wavelengths.
Indium Gallium Arsenide (InGaAs) sensors are the primary sensors used in SWIR, covering typical SWIR band, but can extend as low as 0.550 µm to as high as 2.5 µm.
A large number of applications that are difficult or impossible to perform using visible light are possible using SWIR InGaAs based cameras: nondestructive identification of materials, their composition, coatings and other characteristics, Electronic Board Inspection, Solar cell inspection, Identifying and Sorting, Surveillance, Anti-Counterfeiting, Process Quality Control, etc... When imaging in SWIR, water vapor, fog, and certain materials such as silicon are transparent. Additionally, colors that appear almost identical in the visible may be easily differentiated using SWIR.
MWIR (3-5 μm) and LWIR (8-14 μm) regions are also referred to as “thermal infrared” because radiation is emitted from the object itself and no external light source is needed to image the object. Two major factors determine how bright an object appears to a thermal imager: the object’s temperature and its emissivity (a physical property of materials that describes how efficiently it radiates). As an object gets hotter, it radiates more energy and appears brighter to a thermal imaging system.
Atmospheric obscurants cause much less scattering in the MWIR and
LWIR bands than in the SWIR band, so cameras sensitive to these longer
wavelengths are highly tolerant of smoke, dust, and fog.
MWIR collects the light in the 3 μm to 5 μm spectral band. MWIR cameras are employed when the primary goal is to obtain high-quality images rather than focusing on temperature measurements and mobility. The MWIR band of the spectrum is the region where the thermal contrast is higher due to blackbody physics; while in the LWIR band there is quite more radiation emitted from terrestrial objects compared to the MWIR band, the amount of radiation varies less with temperature: this is why MWIR images generally provide better contrast than LWIR. For example, the emissive peak of hot engines and exhaust gasses occurs in the MWIR band, so these cameras are especially sensitive to vehicles and aircraft. The main detector materials in the MWIR are InSb (Indium antimonide) and HgCdTe (mercury cadmium telluride) also referred to as MCT and partially lead selenide (PbSe).
LWIR collects the light in the 8 μm to 14 μm spectral band and is the wavelength range with the most available thermal imaging cameras. In fact, according to Planck’s law, terrestrial targets emit mainly in the LWIR. LWIR systems applications include thermography/temperature control, predictive maintenance, gas leak detection, imaging of scenes which span a very wide temperature range (and require a broad dynamic range), imaging through thick smoke, etc... The two most commonly used materials for uncooled detectors in the LWIR are amorphous silicon (a-Si) and vanadium oxide (VOx), while cooled detectors in this region are mainly HgCdTe.
Athermalization
Any material is characterized by a certain temperature expansion coefficient and responds to temperature variations by either increasing or decreasing its physical dimensions. Thus, thermal expansion of optical elements might alter a system’s optical performance causing defocusing due to a change of temperature. An optical system is athermalized if its critical performance parameters (such as Modulation Transfer Function, Back Focal Length, Effective Focal Length, …) do not change appreciably over the operating temperature range.
Athermalization techniques can be either active or passive. Active athermalization involves motors or other active systems to mechanically adjust the lens elements’ position, while passive athermalization makes use of design techniques aimed at compensating for thermal defocusing, by combining suitably chosen lens materials and optical powers (optical compensation) or by using expansion rods with very different thermal expansion coefficients that mechanically displace a lens element so that the system stays in focus (mechanical compensation).
Thermal radiation principles
An object reacts to incident radiation from its surroundings by
either absorbing, reflecting or transmitting the radiation incident upon
it.
Therefore:
α + ρ + τ = 1
α = absorption coefficient 0 < α < 1
ρ = reflection coefficient 0 < ρ < 1
τ = transmission coefficient 0 < τ < 1
Blackbody
A blackbody is defined as a perfect radiator which absorbs and re-radiates (as stated by Kirchoff’s law) all radiation incident upon it. For a Blackbody α=1, ρ=0, τ=0.
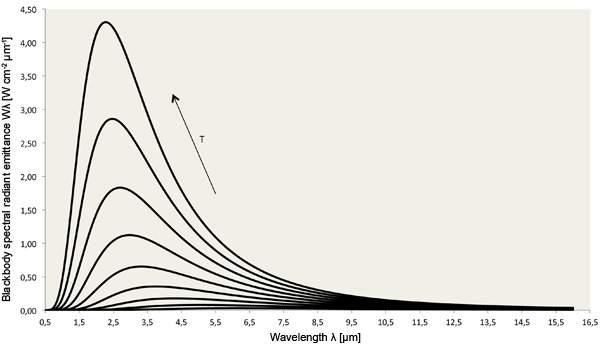
Blackbody spectral radiant emittance (Planck's Law)
Planck’s law describes the spectral radiant emittance of a perfect blackbody as a function of its temperature and the wavelength of the emitted radiation.
The higher the temperature of an object, the higher the spectral radiant emittance (at all wavelengths) and the shorter the peak wavelength of the emissions.
Wλ = Spectral radiant emittance [W cm-2 μm-1]
λ = Wavelength [μm]
T = Blackbody temperature [K]
C1 = 37418 [W μm4 cm-2]
C2 = 14388 [μm K]
e = 2,718…
Stefan-Boltzmann Law
Integrating Planck’s Law we obtain the total radiation of the blackbody at all wavelengths. The resulting equation is known as the Stefan-Boltzmann law and it shows that the power radiated from a blackbody varies as the fourth power of its temperature.
W = Radiant emittance [W cm-2]
T = Blackbody temperature [K]
σ = Stefan-Boltzmann constant 5,67 x 10-12 [W cm2 K4]
Wien displacement Law
In order to find the wavelength at which the the blackbody spectral radiant emittance is at its maximum we should differentiate the Planck’s law and set the result equal to zero.
λmax = Maximum radiant wavelength [μm]
T = Blackbody temperature [K]
The result shows that the wavelength of maximum radiant emittance of a blackbody is inversely proportional to its temperature.
Including this wavelength in Planck’s law we can determine the maxium radiant emittance of the blackbody.
The result shows that the peak radiant emittance of a blackbody varies at the fifth power of its temperature.
Types of radiation sources and emissivity
Real radiation sources are not blackbodies, i.e. some of the energy incident upon them may be reflected or transmitted. Real radiation sources behavior is defined with respect to a blackbody. Each real radiation source is characterized by a parameter called emissivity, which is defined as the ratio of its radiant emittance W1 and the radiant emittance of a blackbody W at the same temperature.
Therefore it is possible to classify radiation sources as follows:
Blackbody: ε = 1
Graybody: ε = constant < 1 (ε does not depend on wavelength)
Selective radiator: ε = f (λ,T)
Emissivity describes the efficiency of a material to radiate infrared energy compared to a blackbody. Real-world objects have emissivity values between 0 and 1 and are selective radiators, which means that their emissivity varies both with wavelength and temperature. Moreover emissivity is also dependent on emission angle, surface treatment and material thickness.
In general, the duller and blacker a material is, the higher is its emissivity. On the other hand, the more reflective a material is, the lower is its emissivity. Therefore, the same material can show extremely different emissivity values depending on the surface treatment. For example polished aluminium, which is highly reflective, has a much lower emissivity than anodized aluminium.
Thermal imaging cameras can calculate an object temperature by
detecting and quantifying the emitted energy over the operational
wavelength range of the detector. Temperature is then calculated by
relating the measured energy to the temperature of a blackbody radiating
an equivalent amount of energy according to Planck’s Blackbody Law.
Because the emissivity of an object affects how much energy an object
emits, emissivity also influences a thermal imager’s temperature
calculation.
Material | Emissivity |
Human Skin | 0,98 |
Water | 0,95 |
Aluminium (polished) | 0,10 |
Aluminium (anodized) | 0,65 |
Plastic | 0,93 |
Ceramic | 0,94 |
Glass | 0,87 |
Rubber | 0,90 |
Cloth | 0,95 |
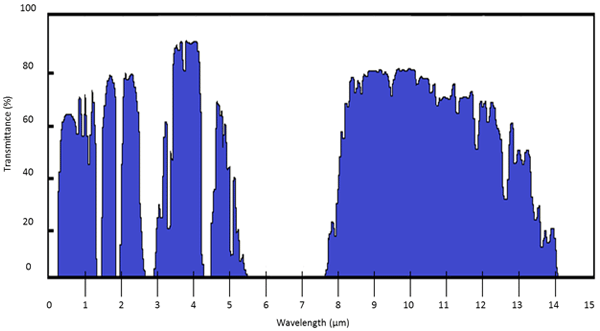
Atmospheric windows
Water vapor and gasses that make up the Earth’s atmosphere tend to absorb infrared radiation coming from an object, which becomes therefore severely attenuated if radiation must be detected at great distances from the object.
Thus, in order to detect the IR signal, one must use the so-called atmospheric windows. Essentially two infrared atmospheric windows (bands) are available: the short/medium-wave windows spanning form 2 to 5,6 μm and the long-wave window, spanning from approximately 7,5 to 14 μm. The composition of the detector’s materials is selected to achieve high sensitivity in one of these bands.