Telecentric lenses

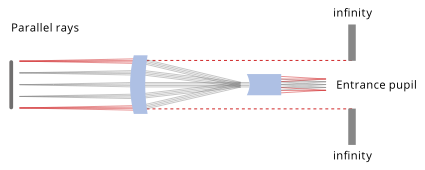
Telecentric lenses represent a special class of optics designed to only collect collimated light ray bundles (i.e. parallel to the optical axis, see picture), thus eliminating perspective errors.

Since only rays parallel to the optical axis are accepted, the magnification of a telecentric lens is independent of the object location. This unique feature makes telecentric lenses perfectly suited for measurement applications, where perspective errors and changes in magnification can lead to inconsistent measurements. Because of its design, the front element of a telecentric lens must be at least as large as the desired FOV, making these lenses inadequate to image very large objects.

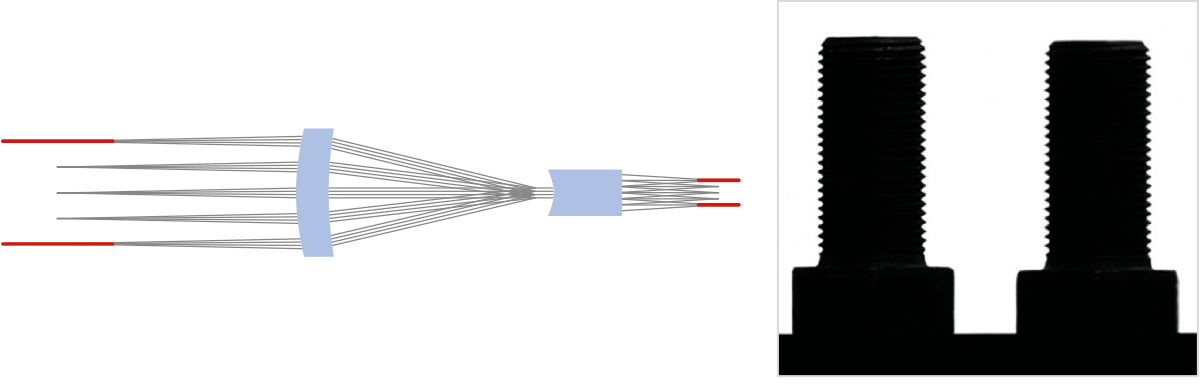
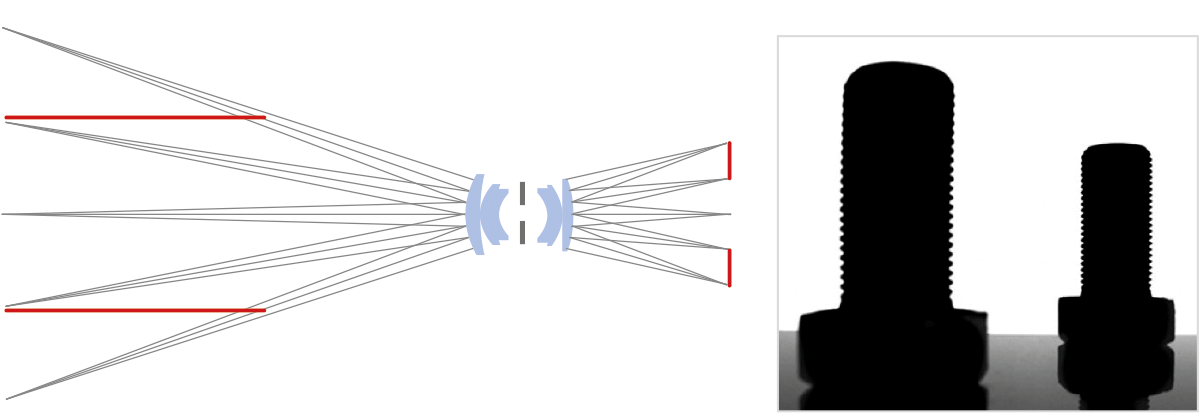
The drawings show the difference between common optics (entocentric) and telecentric lenses. Fixed focal length lenses are entocentric lenses, meaning that they collect rays diverging from the optical axis. This allows them to cover large FoVs but since magnification is different at different working distances, these lenses are not suited to determine the true dimensions of an object.

What is a telecentric lens, and why is it so useful in optical applications? Telecentric lenses are a special class of optics designed to collect only collimated light ray bundles, parallel to the optical axis. This unique feature eliminates perspective errors and ensures consistent magnification, regardless of the object's location.

This makes telecentric lenses ideal for measurement applications, where precise and accurate dimensional analysis is crucial. Unlike conventional lenses, telecentric lenses maintain constant magnification, avoiding distortions caused by changes in working distance.

The illustrations show the distinction between telecentric and common optics (entocentric) lenses like fixed focal length lenses. As entocentric lenses gather rays that are deviating from the optical axis. This enables them to cover a wide field of view, however these lenses are not appropriate for determining an object's actual size because magnification varies with working distance.

Bi-telecentric lenses, which are telecentric in both object and image space, offer even greater accuracy by ensuring symmetrical point spread functions and consistent magnification throughout the depth of field.

Opto Engineering telecentric lenses do not integrate an iris or focusing mechanism. Adjusting the aperture can be easily done upon request before shipping, without additional costs or delays. This design choice minimizes mechanical play and distortion, ensuring optimal performance. Opto Engineering telecentric lenses provide unparalleled accuracy and reliability in optical measurements, making them the ideal choice for precision applications.

Telecentric lenses, with their precision and versatility, play a crucial role in many applications within the machine vision industry. Let's explore some of the most common uses where telecentric lenses excel.

One of the most common applications is the measurement of precision mechanical parts. In industries like automotive manufacturing, telecentric lenses ensure the accurate measurement of components such as shafts, valves, pistons, and engine parts. This warrants accurate dimensional checks in inline and offline applications.

When using milling and turning machine tools the industry relies on specific gauging devices called 'tool presetters' that utilize small telecentric lenses and collimated sources for precise measurement.

In industries dealing with rubber sealings, O-rings, and plastic caps, telecentric lenses shine in non-contact optical measurement techniques. These lenses are essential for maintaining the integrity of delicate components without altering their shape.

But the applications don't stop there. In machine vision, there are unlimited possibilities when checking quality and providing accurate measurements to eliminate defective products in everyday applications.

As discussed previously, In the world of manufacturing and quality control, precision is paramount. Every detail matters, especially in industries where safety and reliability are non-negotiable.

In pharmaceutical manufacturing, telecentric lenses meticulously inspect glass containers, capsules, vials, and more, guaranteeing perfect sealing and damage prevention. Similarly, in the beverage industry, these lenses measure the threads of glass bottle necks with unparalleled precision.

In the electronics industry, telecentric lenses play a crucial role in inspecting connectors, resistors, transistors, and integrated circuits. These lenses ensure that components are manufactured within specified tolerances and that connections are precise and secure.

Telecentric lenses are also making strides in emerging industries. In solar cell manufacturing, Near-Infrared Telecentric lenses are used for integrity checks, while silicon wafers and LCD surfaces benefit from precise imaging.

Telecentric lenses are also employed in particle measurement, high-precision color measurement, photolithography mask measurement, filter control, and even blood analysis and cell counting.

From automotive to pharmaceuticals, electronics to solar energy, telecentric lenses are the go-to solution for precision measurement and defect detection in the machine vision industry. With their unmatched accuracy and versatility, Opto Engineering telecentric lenses continue to push the boundaries of what's possible in the machine vision industry, ensuring that every product meets the highest standards of quality and reliability.

Better Magnification Constancy

Standard telecentric lenses accept ray cones whose axis is parallel to the main optical axis; if the lens is only telecentric in object space, ray cones passing through the optical system reach the detector from different angles depending upon the field position. Moreover, the optical wavefront is completely asymmetric since incoming telecentric rays become non-telecentric in image space. As a consequence, the spots generated by ray cones on the detector plane change in shape and dimension from point to point in image space (the point-spread function becomes non-symmetrical and a small circular spot grows larger and turns elliptical as you move from the image center towards the borders).

Even worse, when the object is displaced, rays coming from a certain field point generate a spot that moves back and forth over the image plane, thus causing a significant change in magnification. For this reason, non-bi-telecentric lenses show a lower magnification constancy although their telecentricity might be very good if measured only in the object space. Bi-telecentric lenses are telecentric in both object and image space, which means that principal rays are parallel not only when entering but also when exiting the lens. This feature is essential to overcome all the accuracy issues concerned with mono-telecentric lenses such as point spread function inhomogeneity and lack of magnification constancy through the field depth.

Increased field depth

Field depth is the maximum acceptable displacement of an object from its best focus position. Beyond this limit, the image resolution becomes poor, because the rays coming from the object can’t create sufficiently small spots on the detector: blurring effect occurs because geometrical information carried by the optical rays spread over too many image pixels.

Depth of field basically depends upon the optics F/#, which is inversely proportional to the lens aperture diameter: the higher the f-number the larger the field depth, with a quasi-linear dependence. Increasing the F/# reduces ray cones divergence, allowing for smaller spots to form onto the detector; however, raising the F/# over certain values introduces diffraction effects which limit the maximum achievable resolution.

Bi-telecentricity is beneficial in maintaining a very good image contrast even when looking at very thick objects (see Fig. 34): the symmetry of the optical system and the rays parallelism help the image spots with staying symmetrical, which reduces the blur effect. This results in a field depth being perceived as 20-30% larger compared to non-bi-telecentric optics.

Even detector illumination

Bi-telecentric lenses boast a very even illumination of the detector, which comes useful in several applications such as LCD, textile and print quality control. When dichroic filters have to be integrated in the optical path for photometric or radiometric measurements, bi-telecentricity assures that the ray fan axis strikes the filter normal to its surface, thus preserving the optical band-pass over the whole detector area.

Having fixed working distance and aperture, telecentric lenses are classified by their magnification and image circle. Choosing the right telecentric lens is easy: we must find the magnification under which the image fit the sensor.

Example. We need to measure the geometrical feature of a mechanical part (nut) using a telecentric lens and a 2048 x 2048, 5.5 µm sensor. The nut is inscribed in a 10 mm diameter circle with 2 mm uncertainty on the sample position. What is the best choice?

Given the camera resolution and pixel size (2048 x 2048 pix, 5.5 µm), the sensor dimensions are calculated to be 11.26 x 11.26 mm.

The FOV must contain a 12 mm diameter circle, hence the minimum magnification required is 0.938X.

The Opto Engineering® TC23009 telecentric lens (M=1.000X, image circle 11 mm) would give a FOV of 11.26 mm x 11.26 mm, but because of mechanical vignetting the actual FOV is only an 11 mm diameter circle. In this case, if a more accurate part placement cannot be guaranteed, a lens with a lower mag or a larger image circle must be chosen. Using the Opto Engineering® TC2MHR016-x lens (M=0.767X, image circle 16.0 mm) we find a FOV of 14.68 x 14.68 mm which is a very close match.

Selecting the right telecentric lens involves careful consideration of several key parameters to ensure optimal performance and accuracy in your application.

First, consider the field of view (FoV), which represents the total area viewable by the lens and captured by the camera sensor. Next, the working distance (WD) defines the distance between the lens and the object where the image is sharpest. Additionally, depth of field (DoF) which indicates the maximum range where the object remains acceptably in focus.

Now let’s evaluate the sensor size, this is calculated by multiplying the pixel size by the sensor resolution. Magnification, is the ratio between sensor size and FoV, which determines the level of detail captured. Lastly, resolution, the minimum distance between distinguishable points, is crucial for accurate measurements.

Having a fixed working distance and aperture, telecentric lenses are classified by their magnification and image circle. Choosing the correct telecentric lens is straightforward. This is done by determining the magnification required to fit the image onto the sensor.

For example, if you need to measure the geometrical features of a mechanical part that has a 10 mm diameter circle with 2 mm of uncertainty on the positioning of the sample while using a 2048 x 2048, 5.5 µm sensor, the optimal choice would be a lens that provides the required FoV of 14mm.

Given the camera resolution and pixel size of (2048 x 2048 pix, 5.5 µm), the sensor dimensions are calculated to be 11.26 x 11.26 mm.

In this example, the Opto Engineering telecentric lens offers a magnification of 1.000X with an image circle of 11 mm. While this lens provides a close match to the required FoV, mechanical vignetting limits the actual FoV to an 11 mm diameter circle.

Alternatively, the Opto Engineering TC2MHRP016-C lens, with a magnification of 0.767X and an image circle of 16.0 mm, offers a FoV of 14.68 x 14.68 mm, providing a very close match.

As you can clearly see in many applications, accurate measurements and excellent performance can be ensured by choosing the appropriate telecentric lens.

When it comes to precision measurement and defect detection in machine vision, choosing the right telecentric lens is crucial. Let's compare classic, compact, and coaxial telecentric lenses to see which one suits your needs best.

The TC series by Opto Engineering sets the standard for telecentric lenses. These lenses offer exceptional telecentricity and minimal distortion, making them ideal for precise measurement applications. They maintain consistent magnification regardless of object distance, ensuring accuracy across a wide range of mechanical parts.

For those seeking compactness without compromising performance, the TC CORE series delivers. These lenses feature a revolutionary ultra-compact design, up to 70% smaller than other double-sided telecentric lenses. With maximum mounting flexibility and easy integration into compact machines, TC CORE lenses offer high-end optical performance in a smaller package. It's a patented technology from Opto Engineering!

For applications requiring homogeneous illumination on flat surfaces, the TCCX series is the answer. These lenses feature integrated coaxial light, perfect for detecting small surface defects on reflective surfaces. With excellent illumination stability and resolution, the TCCX series excels in industries such as electronics, semiconductors, glass, and metal fabrication.

Whether you need unparalleled telecentricity, compact design, or integrated coaxial lighting, Opto Engineering offers a wide range of telecentric lenses to meet your specific requirements.

In the world of machine vision, selecting the right lens can make all the difference. Today, we'll explore three innovative lens technologies by Opto Engineering: Focus Tunable, Flat, and Multi Mag lenses.

First up, the TCEL series combines telecentric optics with liquid lens technology, offering a unique solution to increase depth of field. These lenses excel at maintaining excellent optical performance and minimal distortion across various applications, from electronics to the automotive industry. It's a patent pending technology from Opto Engineering!

Next, we have the TC4K series, tailored for measurement applications using line scan cameras. With a design optimized for tight dimensional constraints, TC4K lenses provide versatility and precision. They seamlessly integrate with LTCL4K illuminators, offering optical combinations suitable for diverse measurement configurations.

Lastly, the TCDP PLUS series introduces dual magnification telecentric lenses, ideal for measuring objects of varying sizes or features. These lenses offer repeatability and cost-efficiency by eliminating the need for recalibration between magnification changes. Plus, they integrate seamlessly with CMHO clamping mechanics and LTCLHP collimated illuminators, simplifying your vision system setup.

So, whether you need increased depth of field, precise measurements in tight spaces, or versatility in magnification, Opto Engineering has the right lens for your machine vision needs.

Why Opto Engineering® telecentric lenses do not integrate an iris?

Our TC lenses don’t feature an iris, but we can easily adjust the aperture upon request prior to shipping the lens, without any additional costs or delays for the customer. The reasons why our lenses don’t feature an iris are so many that the proper question would be why other manufacturers do integrate irises?

• adding an iris makes a lens more expensive because of a feature that would only be used once or twice throughout the product life
• iris insertion makes the mechanics less precise and the optical alignment much worse
• we would be unable to test the lenses at the same aperture that the customer would be using
• iris position is much less precise than a metal sheet aperture: this strongly affects telecentricity
• the iris geometry is polygonal, not circular: this changes the inclination of the main rays across the FOV, thus affecting the lens distortion and resolution
• irises cannot be as well centered as fixed, round, diaphragms: proper centering is essential to ensure a good telecentricity of the lens
• only a circular, fixed, aperture makes brightness the same for all lenses
• an adjustable iris is typically not flat and this causes uncertainty in the stop position, which is crucial when using telecentric lenses!
• iris is a moving part that can be dangerous in most industrial environments. Vibrations could easily disassemble the mechanics or change the lens aperture
• the iris setting can be accidentally changed by the user and that would change the original system configuration
• end-users prefer having fewer options and only a few things that have to be tuned in a MV system
• apertures smaller than what is delivered by OE as a standard will not make sense as the resolution will decay because of diffraction limit; on the other hand, much wider apertures would cause a reduction of the field depth.
• the standard aperture of OE lenses is meant to optimize image resolution and field depth.

Why Opto Engineering® telecentric lenses do not feature a focusing mechanism?

As with the iris, a focusing mechanism would generate a mechanical play in the moving part of the lens, thus making it worse the centering of the optical system and also causing trapezoidal distortion.

Another issue is concerned with radial distortion: the distortion of a telecentric lens can be kept small only when the distances between optical components are set at certain values: displacing any element from the correct position would increase the lens distortion. A focusing mechanism makes the positioning of the lenses inside the optical system uncertain and the distortion value unknown: the distortion would then be different from the values obtained in our quality control process.